Grundgrößen der Elektrotechnik: U, I, R, G, P, W und Q
In der Elektrotechnik tauchen immer wieder die gleichen Größen auf: Spannung U, Stromstärke I, Widerstand R, Leitwert G, elektrische Leistung P, elektrische Arbeit W und elektrische Ladung Q. Diese Größen gelten sowohl für Gleichstrom (DC) als auch – mit kleinen Ergänzungen – für Wechselstrom (AC).
Wichtiger Ausgangspunkt: Im internationalen Einheitensystem (SI) ist die Stromstärke I (Ampere) die einzige elektrische Basisgröße. Alle anderen elektrischen Größen wie Spannung U, Widerstand R, Ladung Q oder Leistung P sind abgeleitet. In der Grundausbildung beginnt man fast immer mit dem ohmschen Gesetz U = R · I. Zuerst betrachten wir Gleichstrom, anschließend wird jeweils kurz erklärt, wie sich das auf Wechselstrom überträgt.
In der Grundausbildung ist U = R · I mit Gleichstrom der Startpunkt. Für einfache Wechselstromfälle (nur Widerstand) gelten dieselben Formeln, wenn man mit Effektivwerten arbeitet (Ueff, Ieff).
Spannung U – elektrische Potenzialdifferenz
Die Spannung U gibt an, wie stark elektrische Ladungen „angetrieben“ werden. Man kann sie sich als elektrischen Druck vorstellen, der Strom durch einen Leiter oder Widerstand treibt. Spannung gibt es nur zwischen zwei Punkten, zum Beispiel zwischen Plus und Minus einer Quelle.
Für einen einfachen Gleichstromkreis (Batterie, Netzteil) gilt: U = R · I. Die Spannung U zwischen zwei Punkten ist das Produkt aus dem Widerstand R zwischen diesen Punkten und der Stromstärke I, die dadurch fließt.
Bei Wechselspannung (AC), zum Beispiel der Netzspannung, ändert sich die Spannung ständig in Form einer Sinuskurve. Für Berechnungen im Alltag verwendet man den Effektivwert: Ueff. In Europa sind 230 V immer als Effektivwert gemeint. Für rein ohmsche Verbraucher (z. B. Heizwiderstand) gilt dann rechnerisch dasselbe Gesetz: Ueff = R · Ieff.

Grundformel (Gleichstrom, ohmsche Last):
U = R · I
Umgestellt nach I bzw. R:
I = U / R und R = U / I
Formale Definition über Energie und Ladung (gilt allgemein):
U = W / Q Spannung ist die Arbeit W, die nötig ist, um die Ladung Q zwischen zwei Punkten zu verschieben.
Einheit:
1 V = 1 J / C Ein Volt ist ein Joule pro Coulomb.
Für Wechselspannung mit rein ohmscher Last werden die gleichen Formeln benutzt, allerdings mit Effektivwerten: Ueff = R · Ieff.
Typische Spannungsbereiche:
- 5–24 V DC: Elektronik, Mikrocontroller, Sensoren.
- 12 V / 24 V DC: Fahrzeugbatterien, Steuerstromkreise.
- 230 V AC: Netzspannung (Effektivwert) in Europa.
In vielen Schaltungen wird Gleichspannung benutzt (z. B. aus Netzteilen), auch wenn die Energie ursprünglich aus Wechselspannung kommt.
Vereinfachte Ausbildungswerte (Normen im Unterricht genauer):
- Bis ca. 50 V AC oder 120 V DC: Schutzkleinspannung – im Normalfall meist nicht lebensgefährlich, aber nicht harmlos.
- Ab ca. 50 V AC bzw. 120 V DC: deutlich erhöhte Stromschlaggefahr.
- Lebensgefährlich werden Spannungen dann, wenn der resultierende Strom durch den Körper im Bereich von etwa 50–100 mA liegt, besonders durch den Brustbereich.
AC ist bei gleichen Effektivwerten in der Regel etwas kritischer für den Menschen als DC, weil Frequenz und Einwirkdauer eine Rolle spielen.
Ein ohmscher Widerstand von R = 220 Ω wird mit einem Strom von I = 0,10 A betrieben (Gleichstrom). Berechne die Spannung U.
1. Ohmsches Gesetz:
U = R · I
2. Einsetzen:
U = 220 Ω · 0,10 A = 22 V
Die Spannung beträgt U = 22 V.
Würde es sich um Wechselspannung mit rein ohmscher Last handeln,
wäre dies der Effektivwert Ueff.
Stromstärke I und Ladung Q – wie viel fließt?
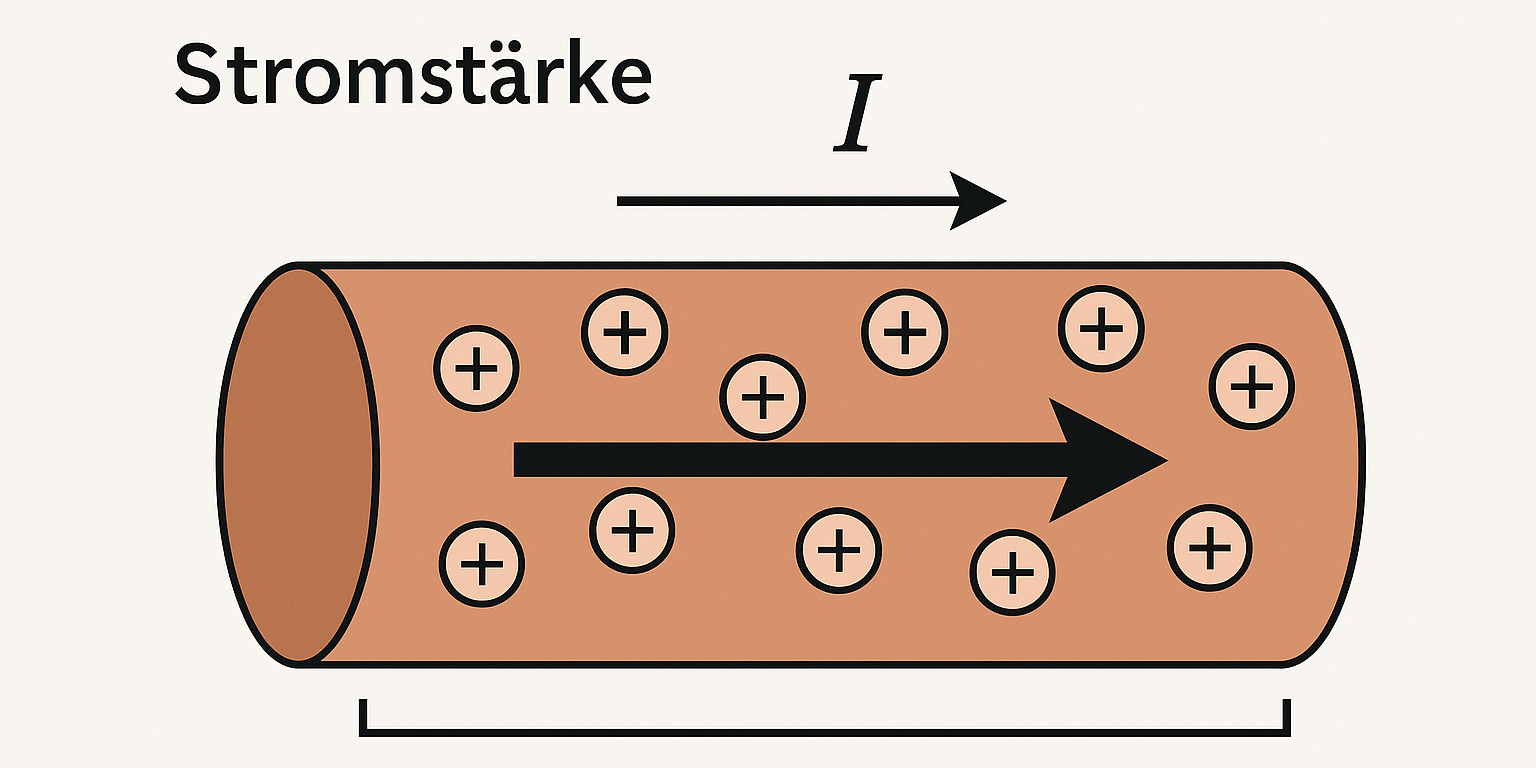
Die Stromstärke I gibt an, wie viel elektrische Ladung pro Sekunde durch einen Leiter oder ein Bauteil fließt. Je größer I, desto stärker werden Leiter, Bauteile und Kontakte belastet (Erwärmung, Verschleiß).
Achtung: Konventionelle Stromrichtung ist von Plus nach Minus definiert. In Wirklichkeit bewegen sich die Elektronen im Metallleiter von Minus nach Plus. In Schaltplänen und Berechnungen arbeitest du immer mit der konventionellen Richtung I (Plus → Minus).
Im Gleichstromkreis berechnest du den Strom mit dem ohmschen Gesetz: I = U / R. Bei Wechselstrom mit rein ohmscher Last gilt dieselbe Formel mit Effektivwerten: Ieff = Ueff / R.
Formale Definition der Stromstärke (gilt allgemein): I = Q / t. I ist die Ladungsmenge Q, die in der Zeit t durch einen Leiterquerschnitt fließt.
Berechnung im (Gleich-)Stromkreis:
I = U / R
Allgemeine Definition:
I = Q / t
Einheiten:
- Stromstärke I: Ampere (A)
- Ladung Q: Coulomb (C)
- Zeit t: Sekunde (s)
Beispiel: Fließen 2 C in 1 s, so ist I = 2 C / 1 s = 2 A. Bei Wechselstrom gibt der Effektivwert Ieff diejenige Stromstärke an, die die gleiche Wärmeleistung wie ein Gleichstrom gleicher Höhe erzeugt.
Typische Bereiche:
- µA–mA: Elektronik, Mess- und Steuertechnik.
- 0,1–16 A: Haushaltsstromkreise (AC).
- Zehner bis Hunderter Ampere: große Motoren, Schweißgeräte, Starter im Kfz.
Für Sicherheitsbetrachtungen ist immer der Strom durch den Körper entscheidend, egal ob er aus Gleich- oder Wechselspannung entsteht.
Stromstärken durch den menschlichen Körper (grobe Richtwerte):
- unter 1 mA: meist kaum spürbar.
- 5–10 mA: deutlich spürbar, Loslassgrenze.
- ab ca. 30 mA: gefährlicher Bereich, Herzrhythmusstörungen möglich.
- 50–100 mA und mehr: hohe Wahrscheinlichkeit lebensbedrohlicher Wirkungen.
Fehlerstromschutzschalter (FI/RCD) mit 30 mA Nennfehlerstrom sollen genau in diesem gefährlichen Bereich schnell abschalten.
An einer Gleichspannungsquelle von U = 24 V liegt ein Widerstand von R = 48 Ω. Berechne die Stromstärke I. Wie würde sich das Ergebnis ändern, wenn es eine 24 V Wechselspannungsquelle mit rein ohmscher Last wäre?
DC-Fall:
I = U / R = 24 V / 48 Ω = 0,5 A
AC-Fall mit rein ohmscher Last:
Auch hier verwendest du Effektivwerte:
Ieff = Ueff / R = 24 V / 48 Ω = 0,5 A
Ergebnis: In beiden Fällen ergibt sich 0,5 A. Der Unterschied liegt in der
zeitlichen Verlaufsform (konstanter Strom vs. sinusförmiger Strom).
Widerstand R und Leitwert G – Strom begrenzen oder ermöglichen
Der Widerstand R beschreibt, wie stark ein Bauteil den Stromfluss behindert. Ein hoher R bedeutet: bei gegebener Spannung fließt wenig Strom. Ein kleiner R bedeutet: bei gleicher Spannung fließt viel Strom.
Das ohmsche Gesetz verknüpft R, U und I: U = R · I. Im Gleichstromkreis gilt das direkt. Bei Wechselstrom gilt es genau so für einen idealen ohmschen Widerstand, wenn man Effektivwerte benutzt (Ueff, Ieff).
Der Leitwert G ist der Kehrwert des Widerstands: G = 1 / R. Je größer G, desto „leitfähiger“ ist das Bauteil. In vielen Rechenaufgaben – besonders bei Parallelschaltungen – ist G praktischer zu verwenden als R.
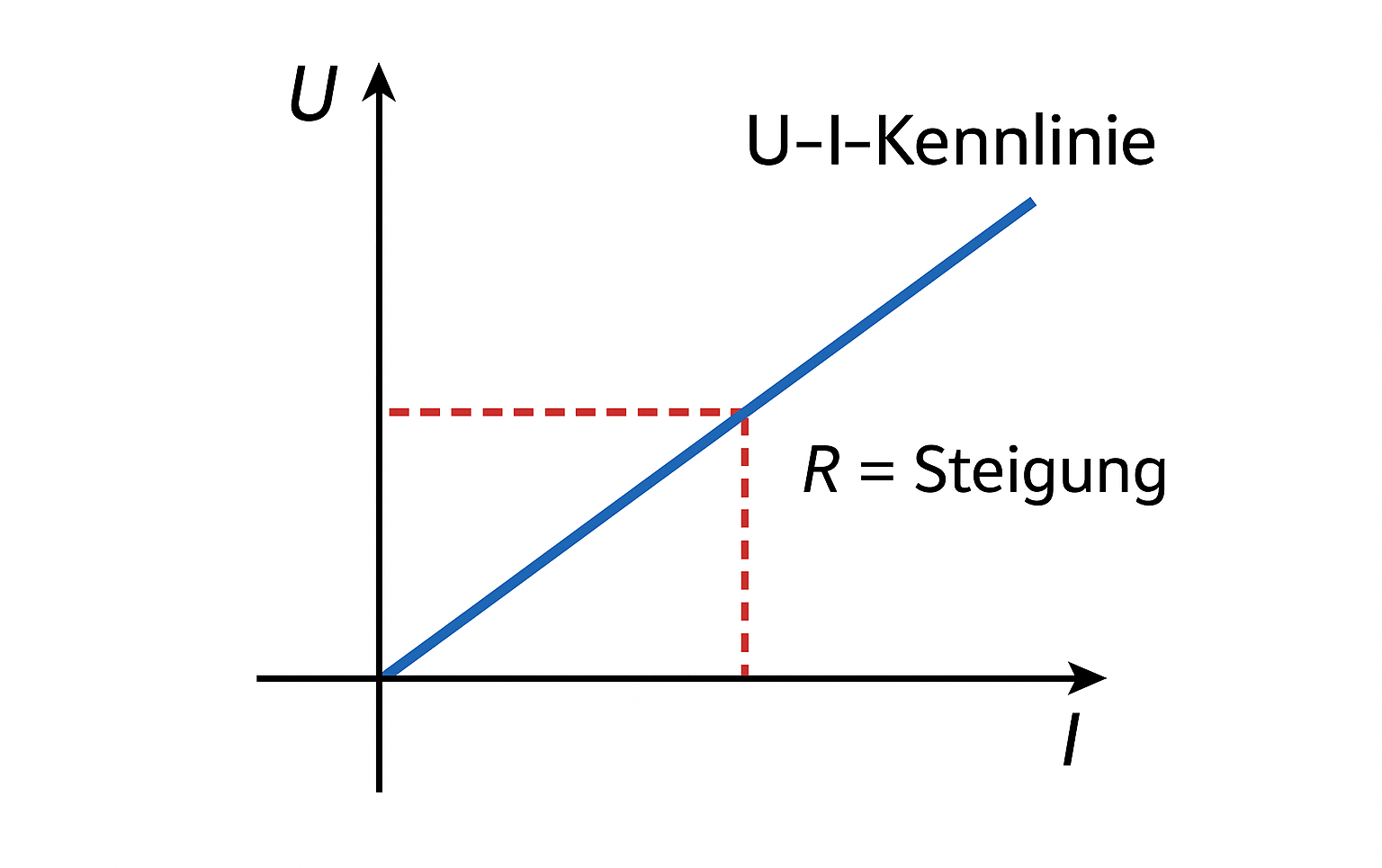
Ohmsches Gesetz:
U = R · I
Umstellung:
R = U / I
Leitwert:
G = 1 / R und I = G · U
Einheiten:
- Widerstand R: Ohm (Ω)
- Leitwert G: Siemens (S)
Für ideal ohmsche Bauteile macht es keinen Unterschied, ob du mit Gleichstrom oder Wechselstrom arbeitest: R ist derselbe, die Formeln gelten in beiden Fällen.
Parallelschaltung mit Leitwerten:
Gges = G1 + G2 + …
und daraus:
Rges = 1 / Gges
Dieser Ansatz funktioniert für Gleich- und Wechselstrom gleichermaßen, solange nur ohmsche Widerstände beteiligt sind (keine Spulen/Kondensatoren).
Ist R zu klein, fließen bei gegebener Spannung hohe Ströme:
- Leiter und Bauteile können überhitzen und beschädigt werden.
- Isolationsschäden und Brandgefahr sind möglich.
- Sicherungen und Leitungsschutzschalter sind auf maximal zulässige Ströme ausgelegt und müssen bei Überstrom auslösen.
Diese Überlegungen gelten sowohl für Gleichstromkreise (z. B. 12 V DC im Auto) als auch für Wechselstromkreise (230 V AC im Haushalt).
An einem unbekannten ohmschen Verbraucher liegt eine Spannung von
U = 18 V. Es fließt ein Strom von I = 0,3 A.
1) Bestimme R.
2) Bestimme G.
3) Wie groß wäre der Strom bei U = 24 V?
1) Widerstand:
R = U / I = 18 V / 0,3 A = 60 Ω
2) Leitwert:
G = 1 / 60 Ω ≈ 0,0167 S
3) Strom bei 24 V (DC oder AC mit rein ohmscher Last):
I = G · U = 0,0167 S · 24 V ≈ 0,4 A
Der Strom steigt von 0,3 A auf etwa 0,4 A.
Elektrische Leistung P und elektrische Arbeit W
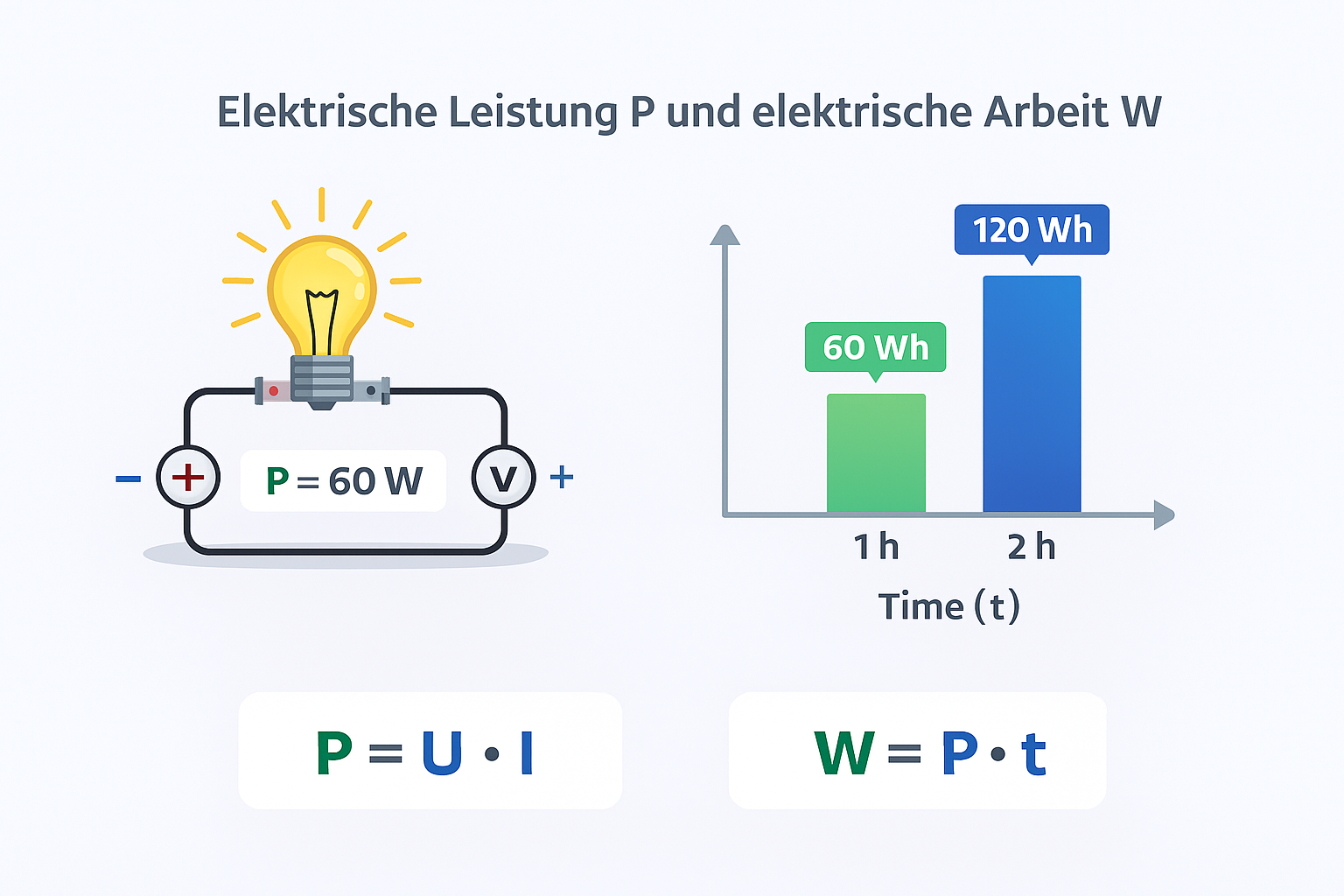
Die elektrische Leistung P beschreibt, wie schnell elektrische Energie umgesetzt wird. Sie zeigt, wie viel Energie pro Sekunde verbraucht oder in andere Formen (Wärme, Licht, Bewegung) umgewandelt wird.
Im Gleichstromkreis kombinierst du das ohmsche Gesetz U = R · I mit der Leistungsformel P = U · I. Bei Wechselstrom mit rein ohmscher Last (z. B. Heizwiderstand) gelten dieselben Formeln mit Effektivwerten: P = Ueff · Ieff.
Ausgangsformeln:
– Ohmsches Gesetz:
U = R · I
– Leistung:
P = U · I
Für Gleichstrom (DC) bzw. AC mit rein ohmscher Last:
P = U · I
P = U² / R (über I = U / R)
P = R · I² (über U = R · I)
Elektrische Arbeit W:
W = P · t
Einheiten:
- Leistung P: Watt (W)
- Arbeit/Energie W: Joule (J)
Zusammenhang: 1 J = 1 W · 1 s Ein Joule ist eine Wattsekunde. In der Energietechnik wird oft die Kilowattstunde verwendet: 1 kWh = 3,6 · 10⁶ J.
Bei allgemeinen Wechselstromkreisen mit Spulen und Kondensatoren kommen noch Blind- und Scheinleistung ins Spiel (cos φ etc.). In diesem Grundkapitel betrachten wir nur reine Widerstände, dort reicht P = Ueff · Ieff.
Typische Leistungsbereiche:
- 5–20 W: kleine Netzteile, Router, LED-Lampen.
- 100–1000 W: viele Haushaltsgeräte (z. B. Staubsauger, Wasserkocher).
- Mehrere kW: Herde, Durchlauferhitzer, große Motoren.
Stromrechnungen geben die elektrische Arbeit in kWh an. Beispiel: Ein 1 kW-Verbraucher, der 3 h läuft, verbraucht 3 kWh.
Hohe elektrische Leistung bedeutet hohe Wärmeentwicklung:
- Haushaltssteckdosen sind meist für 16 A bei 230 V AC ausgelegt (ca. 3,6 kW). Werden mehrere starke Verbraucher an einer Leiste betrieben, ist Überlast möglich.
- Leistungsbauteile (Widerstände, Transistoren, Motoren) müssen über Kühlkörper und Lüfter ihre Wärme abführen.
- Dauerhafte Überlast führt zu Isolationsschäden und Brandgefahr – unabhängig davon, ob die Energie aus DC- oder AC-Quellen stammt.
Eine Heizlast hat einen Widerstand von R = 46 Ω und wird an
einer 230 V-Netzspannung betrieben (AC, reine ohmsche Last, Wert als Effektivwert).
1) Berechne I und P.
2) Wie groß ist W in 3 Stunden? (in kWh)
1) Strom mit ohmschem Gesetz (Effektivwerte):
I = U / R = 230 V / 46 Ω = 5 A
2) Leistung:
P = U · I = 230 V · 5 A = 1150 W = 1,15 kW
3) Arbeit in 3 h:
W = P · t = 1,15 kW · 3 h = 3,45 kWh
Die Heizung verbraucht in 3 Stunden etwa 3,45 kWh.
Aufgaben zu den Grundgrößen
Wähle bei jeder Aufgabe genau eine Antwort aus und klicke anschließend auf „Auswerten“. Jede Aufgabe bringt genau einen Punkt. Korrekte Antworten werden grün, falsche Antworten rot hinterlegt.
